Truncated Backpropagation through Time
This post is a short review of Backpropagation Through Time and Truncated Backpropagation Through Time algorithms with a naive RNN model.
Recurrent Neural Network
- motivation
- handle varying length in samples
- want to share features learned across different positions of sequence data
- forward propagation:
\[ \mathbf{a}^{(t + 1)} = g_a(\mathbf{W_{aa}} \mathbf{a}^{(t)} + \mathbf{W_{ax}} x^{(t)} + \mathbf{b_a}), ~~~ \mathbf{y}^{(t + 1)} = g_y(\mathbf{W_{ya}} \mathbf{a}^{(t)} + \mathbf{b_y}) \]
- note:
- this is a naive RNN model with the simplest architecture
- the parameters are shared across the time steps
- note:
- backpropagation through time
- loss \[ \mathcal{L}^{(t)} (\mathbf{\hat{y}}^{(t)}, \mathbf{y}^{t)}) = -\mathbf{y}^{(t)} \text{ log } \mathbf{\hat{y}}^{(t)} - (1 - \mathbf{y}^{(t)}) \text{ log } (1 - \mathbf{\hat{y}}^{(t)}), ~~~ \mathcal{L} = \sum_{t = 1}^T \mathcal{L}^{(t)} (\mathbf{\hat{y}}^{(t)}, \mathbf{y}^{(t)})\]
- gradient descent on parameters
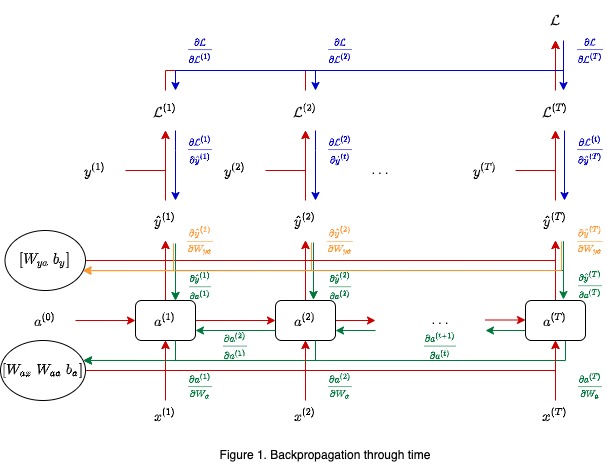
- heavy computational and memory cost:
- need to store hidden states $\{\mathbf{a}^{(t)}\}_{t = 1}^T$
Truncated Backpropagation through Time
- evenly split a long sequence into groups of short sequences, for every $k_1$ forward steps, perform one backward pass over the latest $k_2 ~ (\geq k_1)$ steps, repeat this loop until reaching the end of sequence
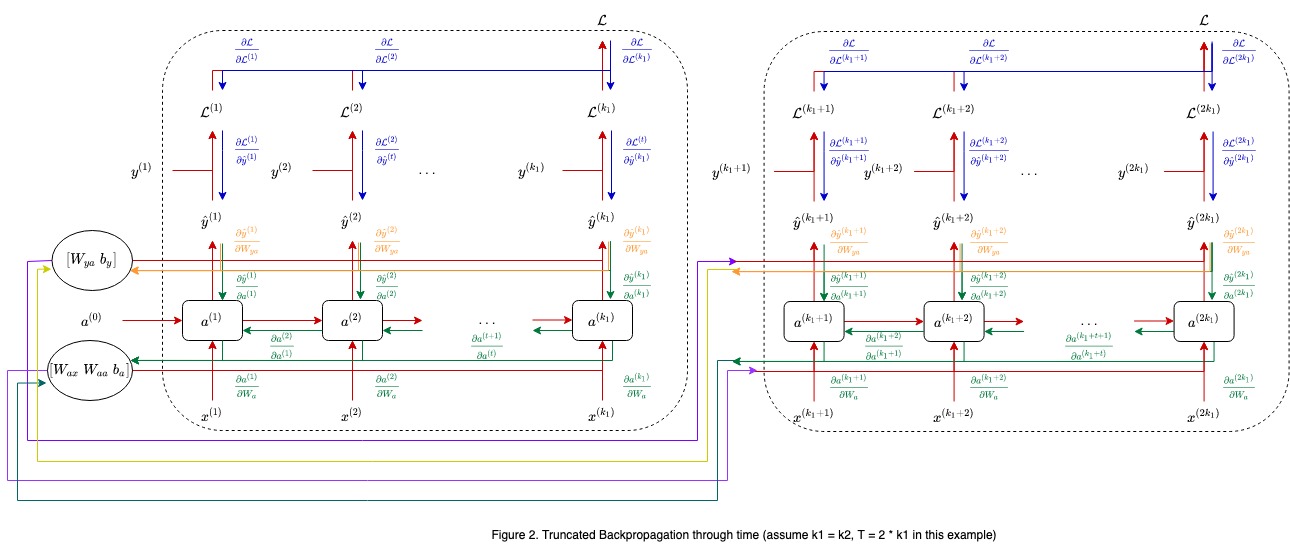
- a practical method to reduce computational and memory cost, but lose long term dependency and has biased gradient estimate
Anticipated Reweighted Truncated Backpropagation (ARTBP)
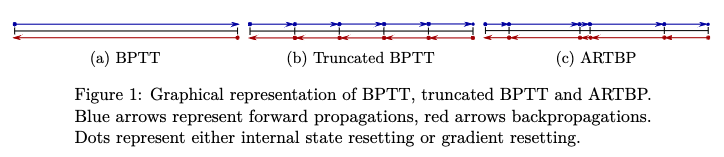
- TODO(bmu)